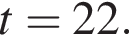Укажите номер рисунка, на котором изображен равнобедренный треугольник.
На клетчатой бумаге с клетками размером 1 см х 1 см изображён параллелограмм. Найдите его площадь в квадратных сантиметрах.
Среди точек
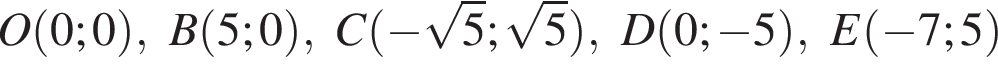 выберите ту, которая принадлежит графику функции, изображённому на рисунке:
выберите ту, которая принадлежит графику функции, изображённому на рисунке:
Найдите значение выражения 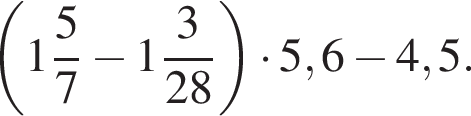
Если 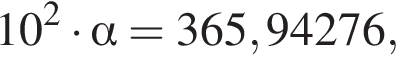 то значение α с точностью до сотых равно:
то значение α с точностью до сотых равно:
На рисунке изображены развернутый угол AOM и лучи OB и OC. Известно, что ∠AOC = 94°, ∠BOM = 126°. Найдите величину угла BOC.
Образующая конуса равна 32 и наклонена к плоскости основания под углом 60°. Найдите площадь боковой поверхности конуса.


От листа жести, имеющего форму квадрата, отрезали прямоугольную полосу шириной 2 дм, после чего площадь оставшейся части листа оказалась равной 15 дм2. Длина стороны квадратного листа (в дециметрах) была равна:
Значение выражения 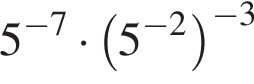 равно:
равно:
Точки A(-1; 3) и B(2 ;5) — вершины квадрата ABCD. Периметр квадрата равен:
Четырехугольник MNPK, в котором ∠N=142°, вписан в окружность. Найдите градусную меру угла K.
На одной чаше уравновешенных весов лежат 3 яблока и 2 груши, на другой — 1 яблоко, 4 груши и гирька весом 40 г. Каков вес одной груши (в граммах), если все фрукты вместе весят 980 г? Считайте все яблоки одинаковыми по весу и все груши одинаковыми по весу.
Прямая a, параллельная плоскости α, находится от нее на расстоянии 2. Через прямую a проведена плоскость β, пересекающая плоскость α по прямой b и образующая с ней угол 60°. Найдите площадь четырехугольника ABCD, если A и B — такие точки прямой a, что AB = 5, а C и D — такие точки прямой b, что CD = 3.
Упростите выражение 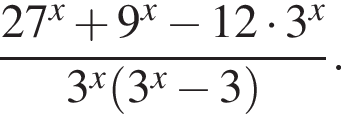
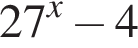
Точки A, B, C лежат на большой окружности сферы так, что треугольник ABC — равносторонний. Если AB = ![]() то площадь сферы равна:
то площадь сферы равна:
В ромб площадью ![]() вписан круг площадью 3π. Сторона ромба равна:
вписан круг площадью 3π. Сторона ромба равна:
Расположите числа 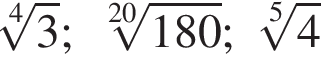 в порядке возрастания.
в порядке возрастания.
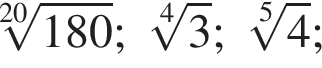

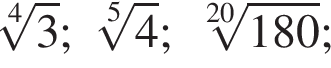
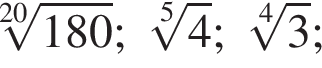
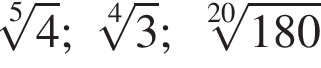
Найдите наименьший положительный корень уравнения 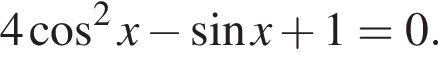

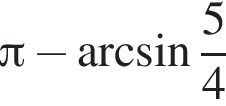
Найдите произведение корней уравнения 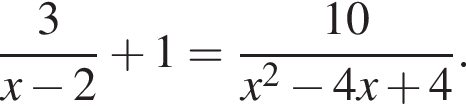
Диагонали трапеции равны 12 и 5. Найдите площадь трапеции, если ее средняя линия равна 6,5.
Найдите модуль разности наибольшего и наименьшего корней уравнения 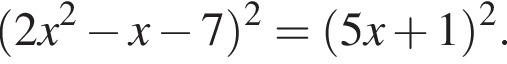
Найдите сумму целых решений неравенства 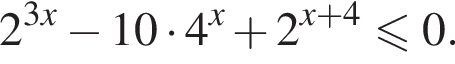
Найдите сумму корней (корень, если он единственный) уравнения 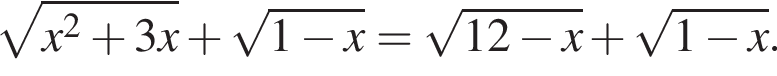
Найдите
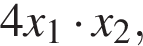 где
где ![]() — абсциссы точек пересечения параболы и горизонтальной прямой (см.рис.).
— абсциссы точек пересечения параболы и горизонтальной прямой (см.рис.).
Четырёхугольник ABCD вписан в окружность. Если 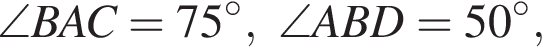 то градусная мера между прямыми AB и CD равна ...
то градусная мера между прямыми AB и CD равна ...
Найдите (в градусах) наибольший отрицательный корень уравнения 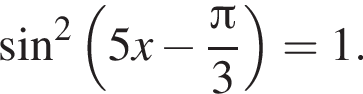
Найдите сумму целых значений x, принадлежащих области определения функции
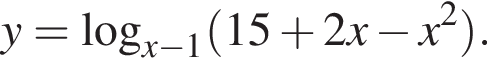
Прямоугольный треугольник с катетами, равными ![]() и
и ![]() вращается вокруг оси, содержащей его гипотенузу. Найдите значение выражения
вращается вокруг оси, содержащей его гипотенузу. Найдите значение выражения ![]() где V — объём фигуры вращения.
где V — объём фигуры вращения.
Если 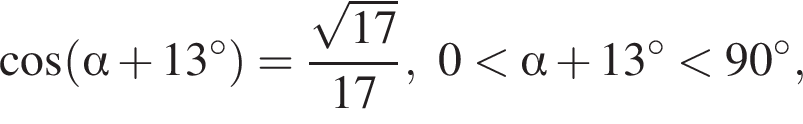 то значение выражения
то значение выражения 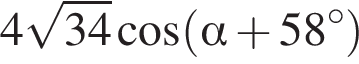 равно ...
равно ...
Найдите произведение корней уравнения 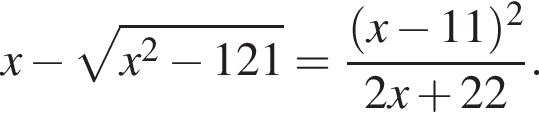

 — все углы разные.
— все углы разные. — все углы разные.
— все углы разные. — треугольник равнобедренный.
— треугольник равнобедренный. — все углы разные.
— все углы разные. — все углы разные.
— все углы разные. см2.
см2.
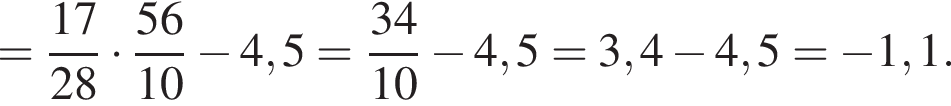
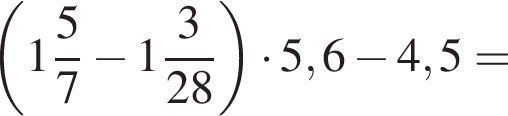
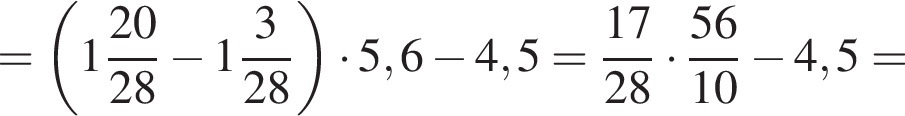
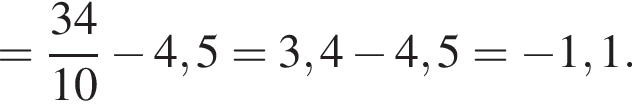
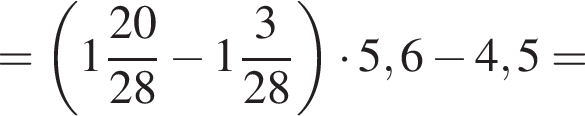
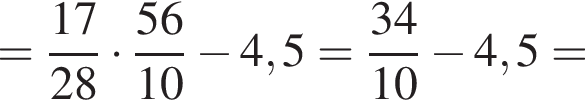
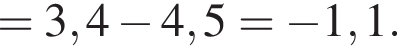
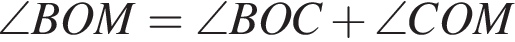 и
и  Таким образом:
Таким образом:
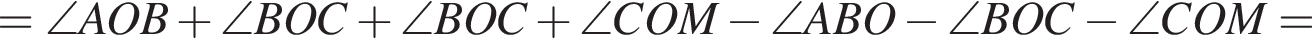

 где r — радиус основания, l — образующая. Найдем радиус:
где r — радиус основания, l — образующая. Найдем радиус:  Таким образом, площадь боковой поверхности равна:
Таким образом, площадь боковой поверхности равна: 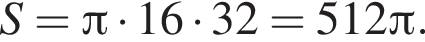
 Тогда:
Тогда: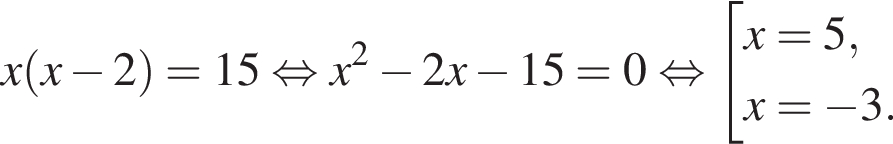

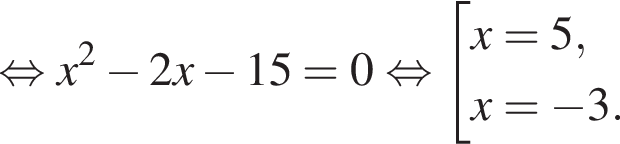
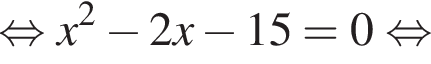
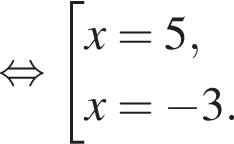
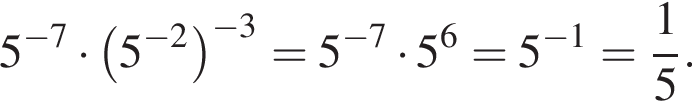
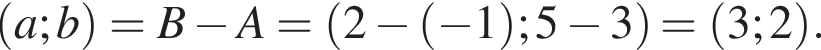
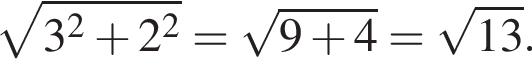 Таким образом, периметр квадрата равен:
Таким образом, периметр квадрата равен: 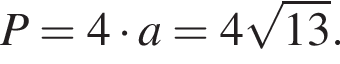

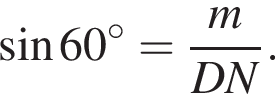
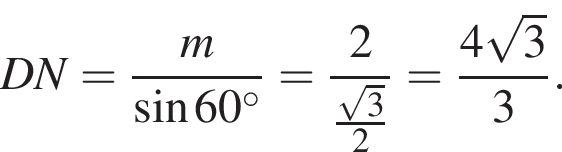
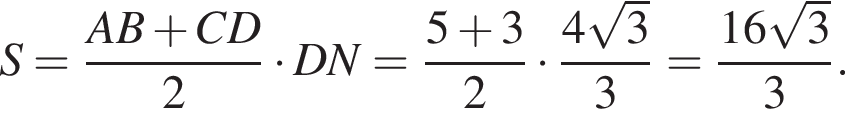
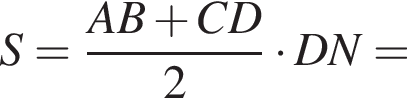
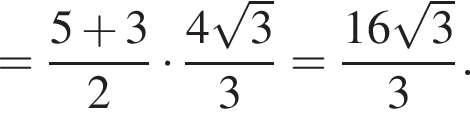
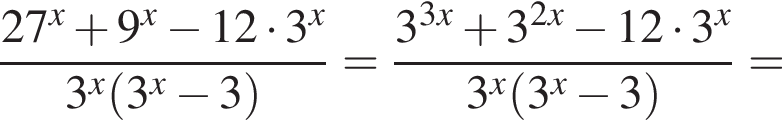
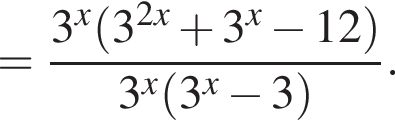
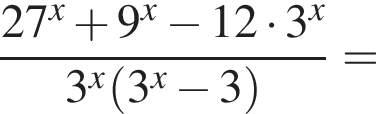
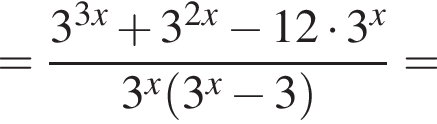
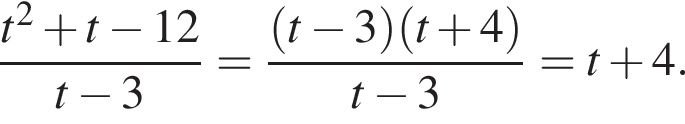 Тем самым, исходное выражение равно
Тем самым, исходное выражение равно 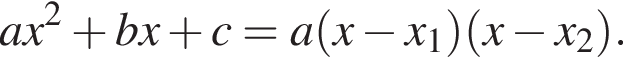
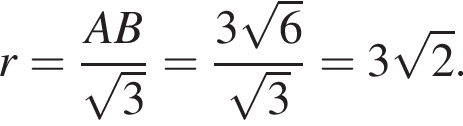 Площадь сферы равна
Площадь сферы равна 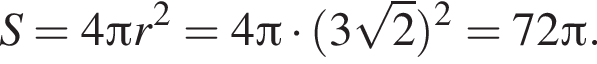
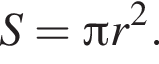 Следовательно, радиус круга равен:
Следовательно, радиус круга равен: 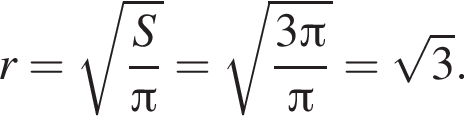 Площадь ромба равна произведению высоты на его сторону:
Площадь ромба равна произведению высоты на его сторону:  Тогда:
Тогда: 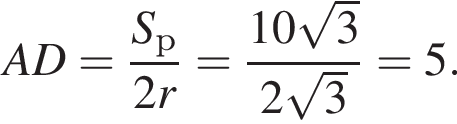
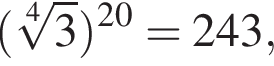
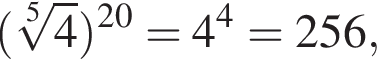
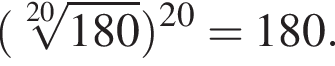
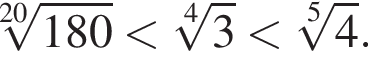
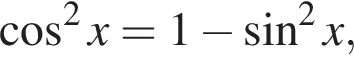 получим:
получим: 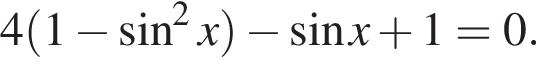 Сделаем замену
Сделаем замену 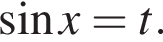 Решим уравнение:
Решим уравнение:
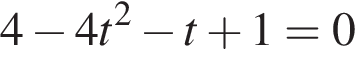
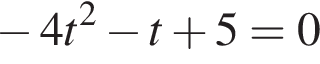
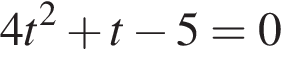
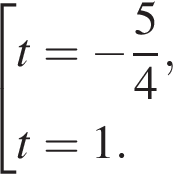
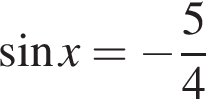 или
или 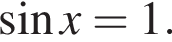 Первое уравнение решений не имеет, поскольку
Первое уравнение решений не имеет, поскольку 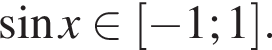 Рассмотрим второе уравнение:
Рассмотрим второе уравнение: 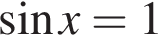
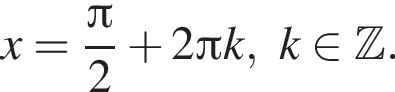
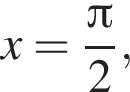 он указан под номером 2.
он указан под номером 2.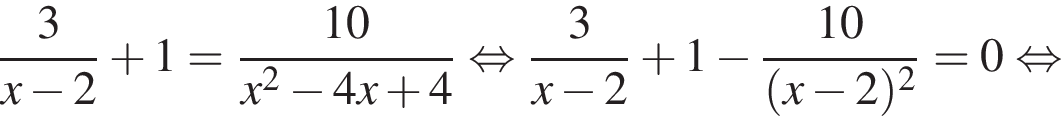
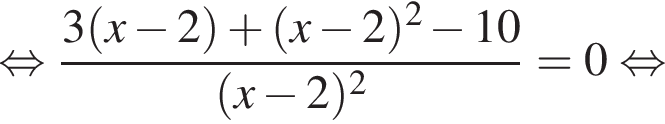
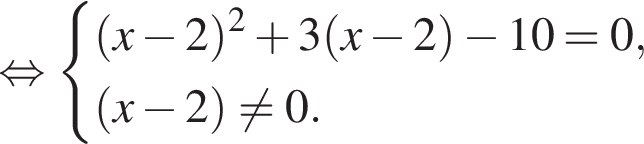
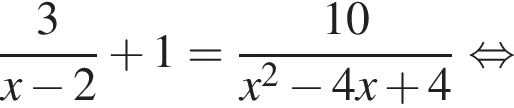
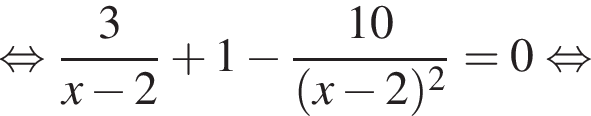
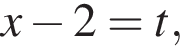 тогда:
тогда: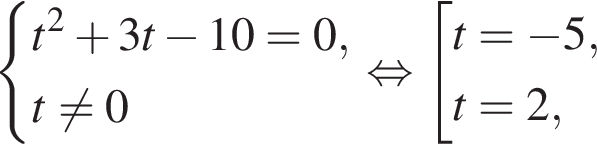
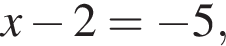 то есть
то есть 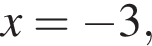 или
или  то есть
то есть 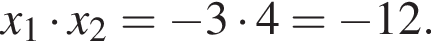
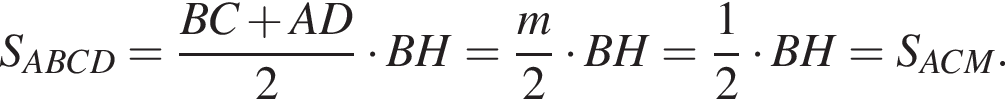
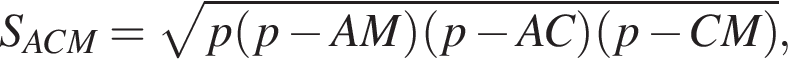 где p — полупериметр треугольника ACM, который равен:
где p — полупериметр треугольника ACM, который равен: 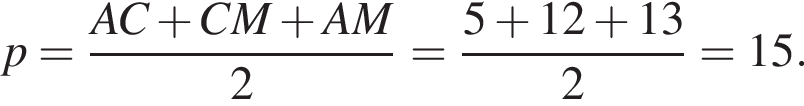
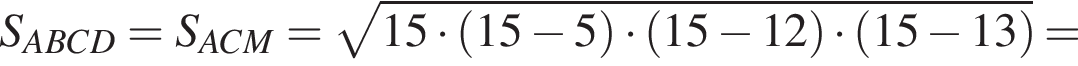
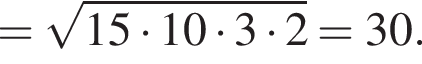
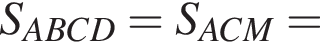
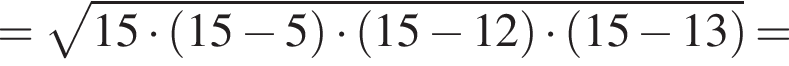
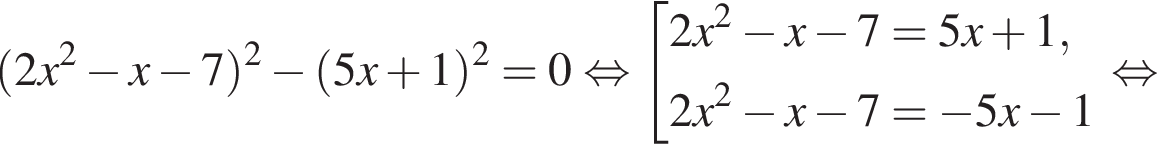
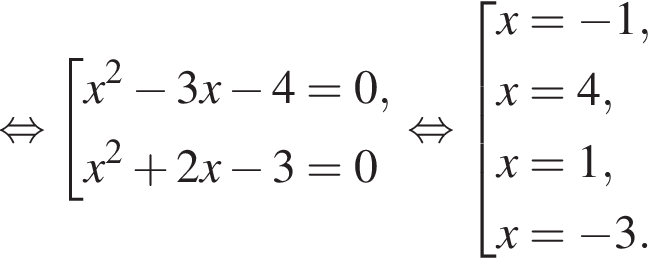
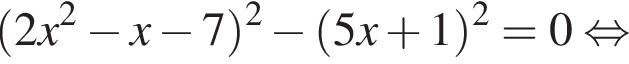
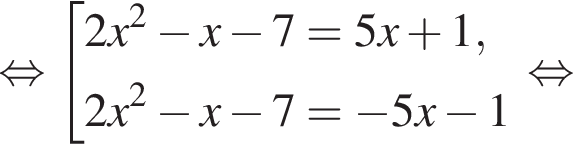
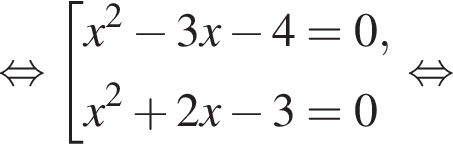
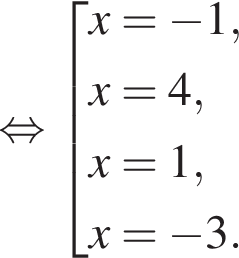
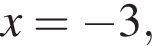 модуль разности наибольшего и наименьшего корней уравнения равен 7.
модуль разности наибольшего и наименьшего корней уравнения равен 7.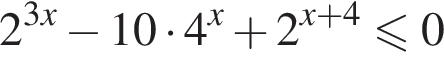
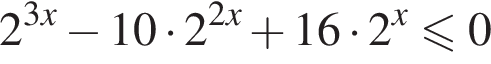
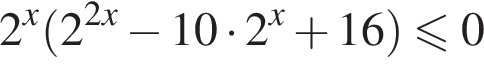
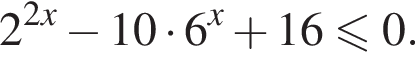
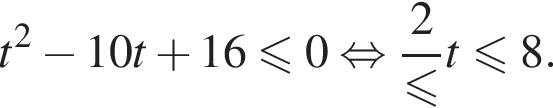
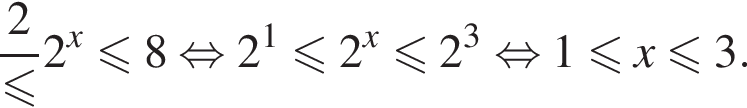
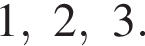 Их сумма равна 6.
Их сумма равна 6.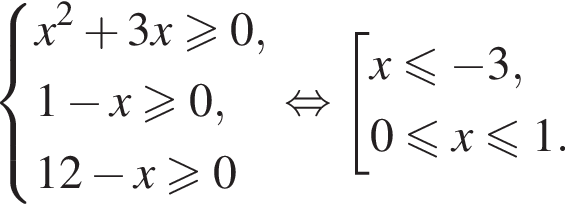
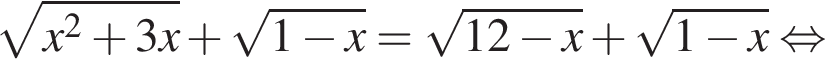
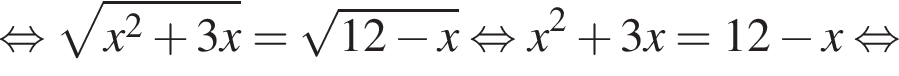
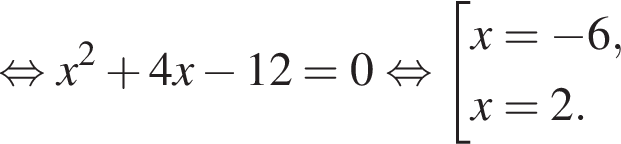
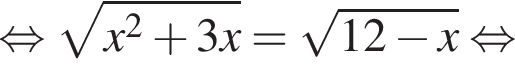
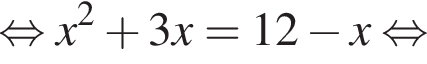
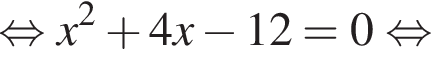
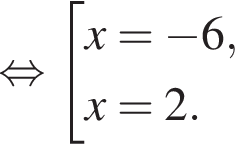
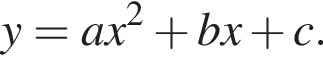 На рисунке изображена парабола с ветвями, направленными вверх, следовательно,
На рисунке изображена парабола с ветвями, направленными вверх, следовательно, 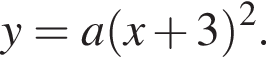 Для того, чтобы найти a, подставим в уравнение параболы точку (-2;1), через которую данная парабола проходит:
Для того, чтобы найти a, подставим в уравнение параболы точку (-2;1), через которую данная парабола проходит: 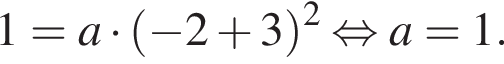 Таким образом, изображённая на графике парабола задается уравнением
Таким образом, изображённая на графике парабола задается уравнением 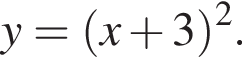
 :
: 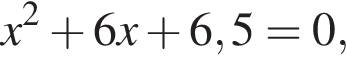 откуда по теореме Виета
откуда по теореме Виета 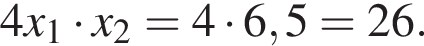


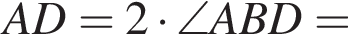

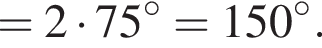
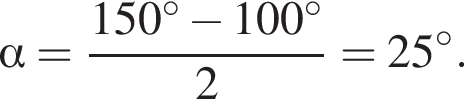
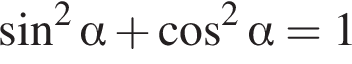 :
: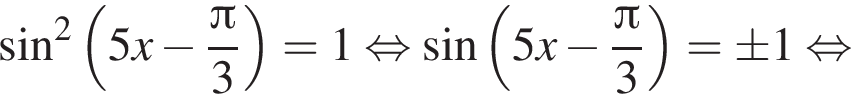
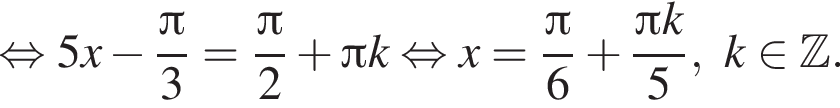
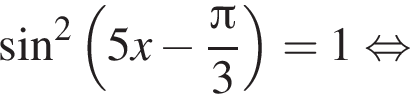
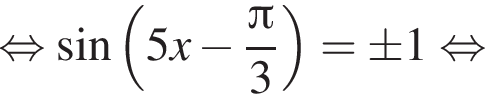
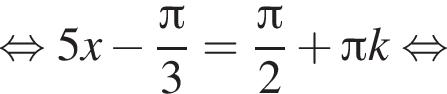
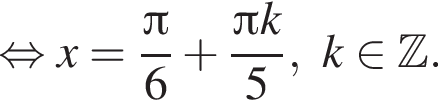
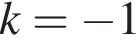 и равен
и равен 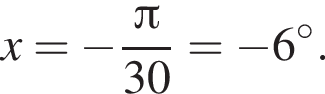
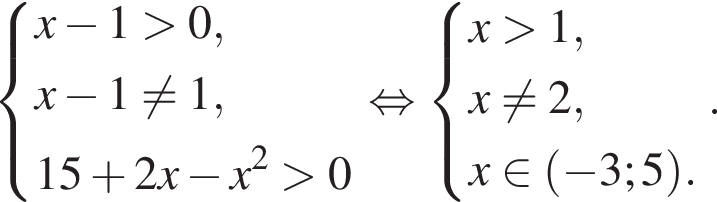
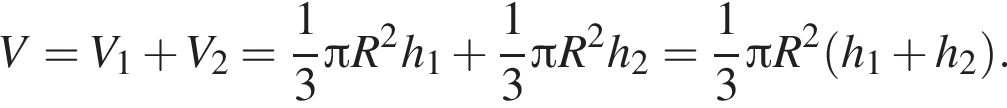
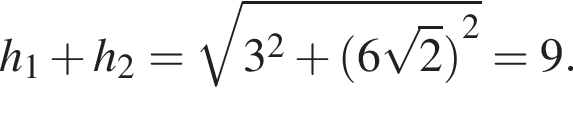 Высота, проведенная из прямого угла, является радиусом конусов и равна:
Высота, проведенная из прямого угла, является радиусом конусов и равна: 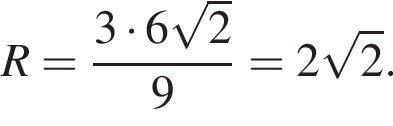 Поэтому:
Поэтому: 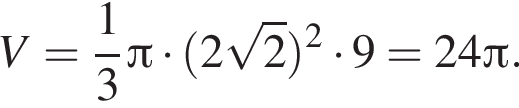
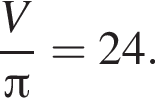
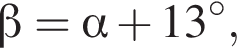 следовательно,
следовательно, 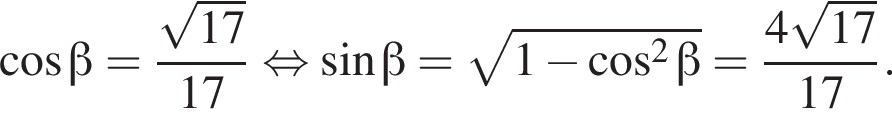
 Таким образом:
Таким образом: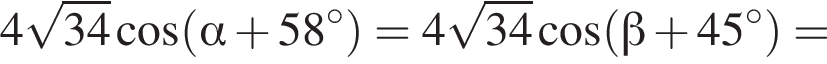
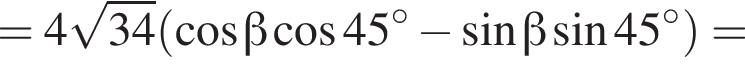
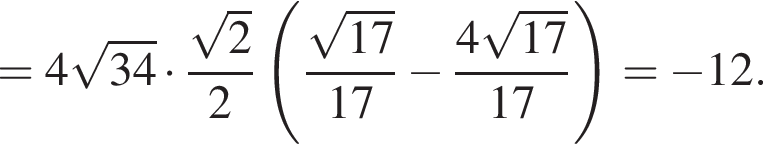
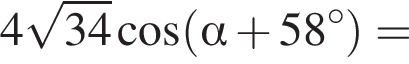
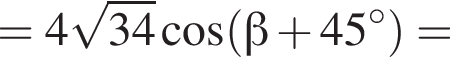

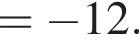
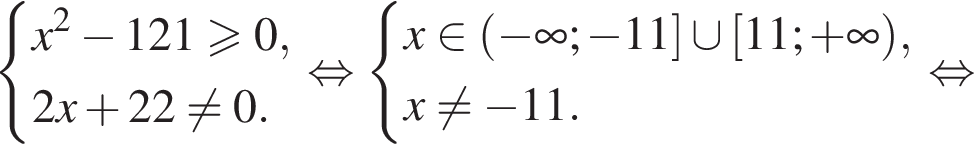
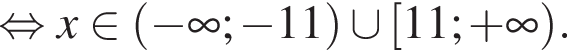
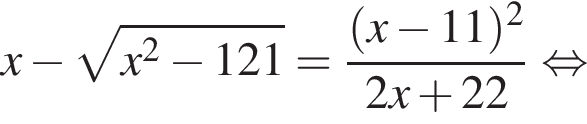
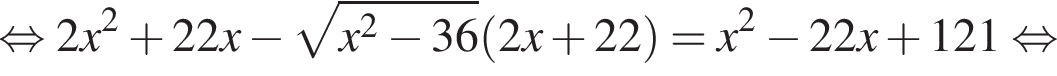
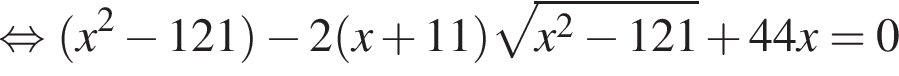
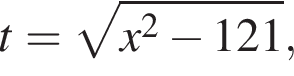 тогда
тогда 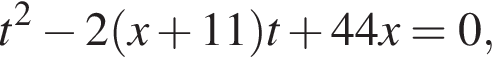 откуда
откуда 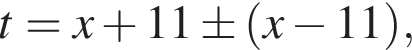 то есть
то есть